Der Holismus besagt, ganz grob, dass das Ganze mehr ist als die Summe seiner Teile. Es gibt ernstzunehmende Gründe für die Annahme, dass verschränkte Quantensysteme in diesem Sinne holistische Systeme sind. Sie stellen damit eine Bedrohung für allgemeine Thesen der Supervenienz und Reduktion dar.

Die Diskussion um den Quantenholismus nimmt ihren Ausgangspunkt bei der  Beschreibung von zusammengesetzten Systemen in der Quantentheorie.

Ein Beispiel für so ein System ist eines aus zwei Protonen. Ein solches System kann nun einerseits über Produktzustände beschrieben werden wie z.B. so:

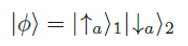
Diese mathematische Formel beschreibt ein aus zwei Systemen zusammengesetztes Gesamtsystem. Dabei kennzeichnen die Indizes "1" und "₂" welchem System der Zustand in der Klammer zukommt. "|↑a⟩₁" besagt z.B., dass das System 1 den Zustand "Spin up" bzgl. der räumlichen Richtung a besitzt. Und "|↓a⟩2" besagt dementsprechend, dass das System 2 den Zustand "Spin down" bzgl. der räumlichen Richtung a besitzt. Angenommen also die Formel beschreibt ein System aus zwei Protonen. Dann sagt sie als Ganzes aus, dass das Proton 1 die Eigenschaft "Spin up" und dass das Proton 2 "Spin down" bezüglich a hat.

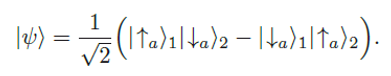
In den meisten Fällen kann man zusammengesetzte Systeme aber nicht durch Produktzustände, sondern nur durch die Superposition von Produktzuständen beschreiben. Das heißt durch sogenannte verschränkte Zustände wie z.B. so:

Die mathematische Formel oben beschreibt den berühmten Singulett-Zustand. Die Indizes "1" und "₂" legen mathematisch nahe, dass es sich hierbei um den Zustand eines Gesamtsystems handelt, das aus zwei Teilsystemen zusammengesetzt ist. Die Formel (2) kann anders als die Formel (1) jedoch nicht in Produktform gebracht werden. Dies bedeutet, dass mathematisch weder dem System 1 noch dem System 2 ein eindeutiger Spinzustand zugeordnet werden kann. Mit anderen Worten: Die Beschreibung des Gesamtzustandes durch "|Ψ⟩"  legt nicht die jeweiligen Spinzustände der einzelnen Teilsysteme 1 und 2 fest.

Wenn man aber Spinmessungen an den Teilsystemen durchführt, erhält man für jedes der Systeme 1 und 2 jeweils eindeutige Messergebnisse. Diese sind zwar zufällig verteilt, es gibt aber gewisse Korrelationen zwischen den Messergebnissen: Wenn man für System 1 den Zustand |↑a⟩₁ misst, liegt nach der Messung am System 2 mit Sicherheit der Zustand |↓a⟩₂ vor und vice versa. Nach der Quantentheorie sind diese Korrelationen unabhängig von der räumlichen Entfernung der Teilsysteme 1 und 2. Insbesondere liegen sie auch dann vor, wenn 1 und 2 raumartig voneinander entfernt sind, d.h. wenn kein Signal zwischen diesen Systemen mit Lichtgeschwindigkeit diese Korrelationen herstellen könnte.

Es gibt grob gesagt zwei mögliche Reaktioenn ...

Stanford Encyclopedia of Philosophy

zum vorherigen Blogeintrag                                       zum nächsten Blogeintrag 

Liste aller Blogbeiträge zum Thema "Quantentheorie"