Dieser Artikel handelt von John Nortons materialen Theorie der Induktion.

Die formale Theorie der Induktion ist so etwas wie die klassische Theorie der Induktion. Sie besagt, dass eine induktive Inferenz dadurch zuverlässig wird,  indem sie eine Instanz eines bestimmten, zuverlässigen Inferenzschemas ist.

Die materiale Theorie der Induktion wurde von John D. Norton in Opposition zu der formalen Theorie der Induktion entwickelt.[1] Nach der materialen Theorie wird eine induktive Inferenz durch spezifische Hintergrundtatsachen zuverlässig.

2003a: Im Gegensatz zu formalen Induktionstheorien behaupte ich, dass es keine universellen induktiven Inferenzschemata gibt. Die induktiven Schlüsse der Wissenschaft sind auf Tatsachen gegründet, die nur in bestimmten Bereichen gelten, so dass alle induktiven Schlüsse lokal sind. Einige sind so lokalisiert, dass sie sich einer vertrauten Charakterisierung entziehen. Da induktive Inferenzschemata durch Fakten belegt sind, können wir das induktive Risiko, das bei einer Induktion eingegangen wird, einschätzen und kontrollieren, indem wir den Haftbefehl auf seine versicherungstechnischen Fakten untersuchen. Indem wir mehr Fakten lernen, erweitern wir unsere induktive Reichweite, indem wir lokalisiertere induktive Inferenzschemata bereitstellen. Da eine materielle Theorie den faktischen und den schematischen Teil einer Induktion nicht mehr trennt, erweist sie sich als nicht anfällig für Humes Problem der Begründung der Induktion.

Es kann zwischen zwei Arten von gültigen Schlüssen unterschieden werden:

1. deduktiv-gültige Schlüsse.

2. nicht deduktiv gültige Schlüsse.

Dabei gilt:

Ein Argument A ist deduktiv gültig, gdw. gilt: wenn die Prämissen von A wahr sind, folgt daraus logisch bzw. notwendig die Wahrheit der Konklusion.

Ein Argument B ist nicht-deduktiv gültig, gdw. gilt: wenn die Prämissen von B wahr sind, folgt daraus nicht logisch auch die Wahrheit der Konklusion. Es ist in dem Fall aber trotzdem rational die Konklusion für wahr zu halten.

ampliativ <-> nicht-demonstrativ. Ampliative Schlussfolgerungen hingegen sind informativ, da sie darauf abzielen, neue Informationen zu liefern. Dies geschieht auf Kosten des Verlustes des notwendigerweise wahrheitserhaltenden Charakters.

Logiker haben mehrere Schemata von deduktiv gültigen Schlüssen formuliert:

Diese Schemata sind universelle deduktive Inferenzregeln. D.h. wir können für "A", "B", "C" beliebige Sätze einfügen. Die Inferenz bleibt immer gültig.

Aber die Deduktion ist konservativ: Die Konklusion sagt uns nicht mehr als das, was uns bereits die Prämissen sagen. Zu sagen, dass alle Menschen sterblich sind und dass alle Griechen Menschen sind, heißt bereits, dass alle Griechen sterblich sind.

Deduktion ist also ein sehr mächtiges Werkzeug, aber es bringt uns nicht sehr weit, wenn es um Überzeugungen über die Welt geht. Die überwiegende Mehrheit unserer Überzeugungen über die Welt wird durch Induktion gebildet (Induktion im weitesten Sinne).

Bei deduktiv zuverlässigen Inferenzschemata --> Aristoteles und ... zitieren.

Viele unserer Überzeugungen werden durch Induktion geformt. Induktion ist amplativ: Die Schlussfolgerung gibt uns mehr Informationen als das, was bereits in den Prämissen enthalten ist.

Bei einem induktiven Argument garantiert die Wahrheit der Prämissen nicht die Wahrheit der Schlussfolgerung. nicht-demonstrativ. Vielmehr macht es die Schlussfolgerung wahrscheinlich oder rational akzeptabel.

Philosophen haben versucht, die induktiv starken Schemata zu artikulieren. Z.B. aufzählende Induktion:

Dies sind vorgeschlagene universelle Induktionsregeln, analog zu den universellen Deduktionsregeln. Wie beim Abzug können Sie "F" und "G" beliebig ersetzen.

Mit der Induktion sind (im Großen und Ganzen) zwei Projekte verbunden: Beschreibung und Begründung.

- Das deskriptive Projekt versucht zu artikulieren, was die induktiven Regeln tatsächlich sind.

- Das Rechtfertigungsprojekt [normative Projekt?] versucht zu zeigen, dass Induktion im Allgemeinen gerechtfertigt ist.

Philosophen konzentrieren sich oft auf das Rechtfertigungsprojekt. Es gibt verschiedene skeptische Herausforderungen an die Induktion (z. B. das Humes-Problem), und diese treten unabhängig von den induktiven Regeln auf.

Aber auch das beschreibende Projekt war nicht besonders erfolgreich. - Es gibt nicht einmal eine Einigung über die grundlegendsten Regeln. Die zuvor angegebene Aufzählungsregel erlaubt eine Vielzahl dummer Schlussfolgerungen:

P1. Verity ist bisher jedes Jahr größer geworden.
K1. Also wird Veritys Größe nächstes Jahr zunehmen.

Im Gegensatz dazu haben wir bei der Deduktion schon vor langer Zeit einen Konsens über eine Vielzahl deduktiver Regeln erzielt. Syllogismen des Aristoteles, Aussagenlogik, Modallogik, ...

Laut John Norton liegt der Fehler hier darin, an Induktion zu denken, indem man die Anwendung universeller Schlussregeln einschließt.

Literaturverzeichnis
Norton, John D. (2005). A Little Survey of Induction. In: Peter Achinstein (Hrsg.): Scientific Evidence: Philosophical Theories and Applications. Baltimore: Johns Hopkins University Press, S. 9 – 34.

Norton, John D. (2006). Induction without Probabilities. Preprint. <http://philsci-archive.pitt.edu/3107/>
Norton, John D. (2010a). Deductively Definable Logies of Induction. Journal of Philosophical Logic 39(6), S. 617 - 654.
Norton, John D. (2010b). A Survey of Inductive Generalization. Preprint. <https://sites.pitt.edu/~jdnorton/papers/Survey_ind_gen.pdf>
Norton, John D. (2010c). There are no Universal Rules of Induction. Philosophy of Science 77(5), S. 765 – 777.

Norton, John D. (2019). A Demonstration of the Incompleteness of Calculi of Inductive Inference. British Journal for the Philosophy of Science 70(4), S. 1119 - 1144.

-

Deduktive und induktive Inferenzschemata:
John Norton. A Material Theory of Induction (2003a):
S. 647: All this can change. In the late nineteenth century, some one hundred years after Bayes made his formula known, the leading systematization was the methods catalogued by Bacon, Herschel and, most precisely, Mill. This instability stands in strong contrast to deductive logic. The deductive syllogisms identified by Aristotle remain paradigms of deduction, with their very dreariness a mark of their unchallenged security.
S. 648: We have been misled, I believe, by the model of deductive logic into seeking an account of induction based on universal schemas.

Es gibt keine Induktionsregeln, keine formalen Schemata, die die guten induktiven Schlüsse von den basinduktiven Schlüssen unterscheiden. Induktive Schlussfolgerungen werden durch bestimmte Fakten lizenziert, nicht durch Regeln. Wie Norton es ausdrückt, ist jede Induktion "lokal".

Betrachten Sie diese beiden induktiven Argumente (zwei Instanzen des Aufzählungsschemas):
SIEHE: John Norton. A Material Theory of Induction (2003a, S. 649):

(A) Diese Wismutproben schmelzen bei 271°C. Alle Wismutproben schmelzen also bei 271 °C.

(B) Diese Wachsproben schmelzen bei 50°C. Alle Wachsproben schmelzen also bei 50°C.

à Also, im ersten Fall, sagt Norton, ist dies eine ziemlich starke Schlussfolgerung. Und wir können uns sogar vorstellen, dass die Anzahl der Messungen ziemlich gering ist, wir könnten annehmen, dass der Wissenschaftler den Schmelzpunkt von gerade gemessenen (Reabilität) 10 Wismutproben gemessen hat.

Norton sagt, dass (A) ein starker induktiver Schluss ist, aber (B) schwach ist. Sie haben jedoch die gleiche Form. Was erklärt den Unterschied?

Aus Sicht des früheren und formalen Induktionsansatzes gibt es hier ein Rätsel. Beide sind Fälle derselben Art von induktiver Argumentform (enumerative Induktion), aber eine ist gerechtfertigt und die andere nicht.

John Norton: Der Unterschied liegt in den Hintergrundfakten. (A) ist gerechtfertigt, weil wir wissen, dass Proben von Elementen in schmelztemperaturrelevanten Eigenschaften einheitlich sind (Einwand: bei kategorialen Eigenschaften multiple Realisierbarkeit von kausalen Rollen).

Für Wachs gibt es diese Tatsache nicht. "Wachs" bezieht sich auf verschiedene Mischungen von Kohlenwasserstoffen. Wachse aus verschiedenen Fabriken können unterschiedliche Schmelzpunkte haben.

Induktive Inferenzen sind nicht durch ihre Form lizenziert. „Einige Fs sind Gs, also sind alle Fs Gs“ ist kein universelles Schema. Es ist nur anwendbar, wenn es durch Tatsachen lizenziert ist.

Das heißt, die Tatsache, dass bestimmte Eigenschaften von Elementen einheitlich sind, erlaubt die Verallgemeinerung von einigen Proben auf alle.

Ein anderes Beispiel: Ein Chemiker stellt ein neues Salz her und gibt seine kristalline Form an. Dies wird insofern induktiv sein, als sie den Bericht als eine Beschreibung der Form des Salzes im Allgemeinen auffassen wird, nicht nur ihrer speziellen Probe.

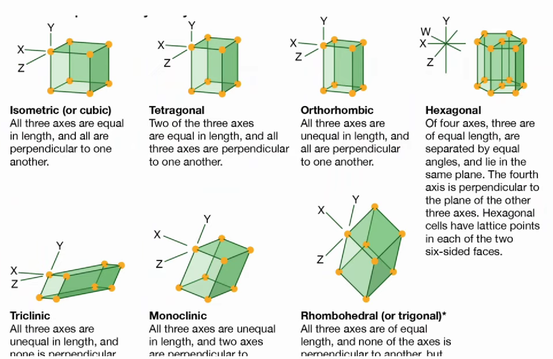
à Im Allgemeinen passen also Instanzen aller kristallbildenden Substanzen in ein einziges charakteristisches kristallographisches (?) System. Die Kristalle werden unterschiedliche Formen haben, aber diese Formen werden alle eine abstraktere Form instanziieren – die sieben verschiedenen Formen oder Systeme werden hier gezeigt. In diesem Schema werden Kristalle auf der Grundlage der für ihre Form charakteristischen Achse in Formen eingeteilt. Nun, für jede Substanz werden ihre Kristalle in einem dieser sieben Systeme sein. Und das geschieht, weil für jede Substanz, die Kristalle bildet, die Kristalle aus sich wiederholenden Einheitszellen aufgebaut sind – Ansammlungen von Atomen, die die gleiche Form haben.

Der hier links(?) gezeigte Kristall hat also eine kubische Form, er ist aus vielen zusammengesteckten Würfeln aufgebaut. Die Form des Kristalls wird durch die Form seiner Elementarzellen bestimmt – und im Allgemeinen basieren alle kristallbildenden Substanzen auf denselben Elementarzellen.

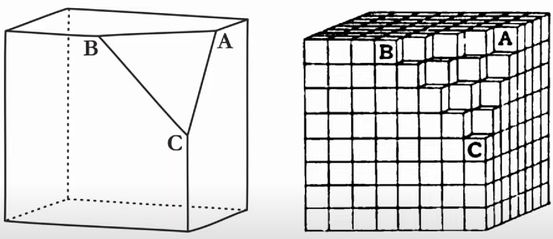
Ø  Ein paar Fs sind Gs, also sind alle Fs Gs.

Ø  Ein paar RaCl2-Kristalle sind monoklin, also sind alle RaCl2-Kristalle monoklin.

"G" kann nicht durch beliebige Kristalleigenschaften ersetzt werden. Wir folgern insbesondere, dass alle Kristalle des Salzes monoklin sind. Dies wird durch die bekannten Tatsachen genehmigt.

Diese Instanz war nicht ganz sicher, weil wir manchmal Polymorphismus finden. Wo die gleichen Substanzen unterschiedliche Kristallinformen erzeugen. Das Hauptrisiko von Marie Curies Schlussfolgerung war also die Möglichkeit des Polymorphismus. Dieses Risiko wurde für Curie verringert, da beobachtet wurde, dass Radiumchlorid sehr ähnliche chemische Eigenschaften wie Bariumchlorid hat und bei Bariumchlorid kein solcher Polymorphismus beobachtet wurde.

Die Tatsache, dass eine Induktion genehmigt wird, ist das "materielle Postulat" der Induktion. Das materielle Postulat von Curies Schlussfolgerung war, dass im Allgemeinen Kristalle bestimmter Substanzen alle Teil eines einzigen kristallographischen Systems sind.

Nach der Materialtheorie ist, sobald Sie die Tatsachen zitiert haben, die eine Induktion zulassen, das alles, was über Induktion zu sagen ist. Es gibt keine allgemeinen Regeln, nur bestimmte Tatsachen, die bestimmte Schlussfolgerungen zulassen.

"Warum ist Curies Schlussfolgerung gerechtfertigt?" – wir antworten nicht, indem wir zeigen, dass sie eine allgemeine Regel verkörpert, sondern indem wir die Tatsachen aufzeigen, auf denen sie beruht.

Literatur
Norton, John D. (2003a). A Material Theory of Induction. Philosophy of Science 70(4), S. 647 - 670.
WEITERES BEISPIEL: Norton, John D. (2007). History of Science and the Material Theory of Induction: Einstein’s Quanta, Mercury’s Perihelion. European Journal for Philosophy of Science 1(1), S. 3 – 27.

Norton, John (2021). The Material Theory of Induction. Calgary: University of Calgary.

Gegeben von John Norton [21.00min].

Kein Versuch, die induktiven Regeln zu artikulieren, die wir angeblich verwenden, war erfolgreich. Selbst über die grundlegendsten induktiven Regeln gibt es keine Einigkeit. Wir werden einige derzeit beliebte Vorschläge berücksichtigen ...

Erstens, der Schluss auf die beste Erklärung. In IBE schlagen wir eine Vielzahl von Theorien zu einigen Phänomenen vor, beurteilen diese Theorien anhand einer Reihe von erklärenden Tugenden und schließen dann auf die Theorie, die am besten funktioniert.

IBE wurde als allgemeines, universelles induktives Schema vorgeschlagen. Es berücksichtigt die aufzählende Induktion in Fällen, in denen diese Regel anwendbar ist.

Wir machen eine Verallgemeinerung von „alle beobachteten Fs waren Gs“ zu „alle Fs sind Gs“, wenn diese Schlussfolgerung die beste Erklärung ist.

Obwohl viele Schlussfolgerungen als IBE interpretiert werden können, könnten wir uns Sorgen machen, dass dies daran liegt, dass IBE einfach zu vage ist.

Nach welchen Maßstäben ist eine Erklärung besser als eine andere? Was ist überhaupt eine Erklärung? Darüber besteht kein Konsens.

Wenn Wissenschaftler zu zeigen versuchen, dass eine Theorie ihren Konkurrenten überlegen ist, sind sie dann wirklich ansprechende Erklärungen? Norton sagt, dass die Verteidigung einer Theorie normalerweise Folgendes beinhaltet:

(1) Zeigt, dass die verfügbaren Beweise angesichts der gemeinsamen Hilfsannahmen den Konkurrenten widersprechen. Die Newtonsche Mechanik konnte die Daten der Merkurbahn nicht verarbeiten, die Allgemeine Relativitätstheorie schon; dies unterstützte also die allgemeine Relativitätstheorie.

(2) Zeigen Sie, dass die Konkurrenten umstrittene Hypothesen aufstellen, für die es keine Beweise gibt. Lyell unterstützte den Uniformitarismus, indem er zeigte, dass die katastrophistische Alternative eine Menge substanzieller, aber nicht unterstützter Behauptungen aufstellte.

Dies kann in Begriffen der allgemeinen Relativitätstheorie und des Uniformitarismus formuliert werden, die "bessere Erklärungen" von Phänomenen liefern als ihre Rivalen. Aber das ist nur vage und verschleiert die tatsächlichen Beweise und Argumente.

Was als beste Erklärung gilt, wird in jedem Fall immer von Hintergrundfakten bestimmt.

Eine Studie zum Heilkraftgebet kommt zu statistisch signifikant positiven Ergebnissen. Was ist die beste Erklärung dafür?

Wenn wir bereits davon ausgehen, dass Gott existiert und auf verschiedene Weise in die Welt eingreift, werden wir uns natürlich darauf berufen, um die Ergebnisse der Studie zu erklären. Ein Atheist würde das ganz anders sehen!

Zweitens, Bayesianismus. Beweis E bestätigt eine Hypothese H nur für den Fall, dass E die Wahrscheinlichkeit von H erhöht, also: P(H|E) > P(H). Wir berechnen P(H|E) mit dem Satz von Bayes:

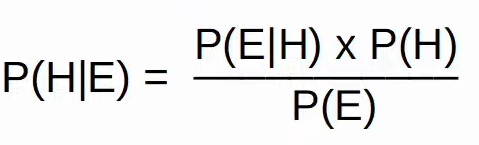
Beispiel: Ich bekomme einen HIV-Test und das Ergebnis ist positiv. Der Test hat eine Rate von 1 % falsch-negativ falsch und 2 % falsch-positiv. Wie hoch ist die Wahrscheinlichkeit, dass ich HIV habe?

P(pos|HIV) = 0,99.
P(HIV) = 0,001.

P(pos) is calculated from (Ppos|HIV) and P(pos|¬HIV).
0,1% of people are HIV+; 99% get a positive result.
99,9% of people are not HIV+, 2% get a positive result.
(0,001*0,99) + (0,999 x 0,02) = 0,02097.

So P(pos|HIV) = 0,99, P(HIV) = 0,001, and P(pos) = 0,02097. Plugging these numbers into Bayes´ theorem, P(HIV|pos) = 0,047.

Wenn ich jedoch mehrere dieser Tests machen würde und sie alle positiv wären, wäre P(HIV|pos) natürlich viel höher.

Der Bayesianismus ist in solchen Kontexten ein mächtiges Werkzeug. Die Bayessche Erkenntnistheorie versucht, den Bayesschen Rahmen auf alle wissenschaftlichen Schlussfolgerungen auszudehnen.

Das Hauptproblem für den Bayesianer ist, wo genau bekommen wir die Zahlen her?

Wir brauchen P(H). Aber das ist die vorherige Wahrscheinlichkeit von z.B. unterbrochenes Gleichgewicht oder das Urknallmodell? Es ist nicht klar, wo man überhaupt anfangen soll, diese Wahrscheinlichkeiten zu berechnen.

Wir brauchen P(E). Wie groß ist die Wahrscheinlichkeit, dass Beweise für eine Hypothese vorliegen, bevor diese Beweise gesammelt werden? Z.B. Wie groß war die Wahrscheinlichkeit der kosmischen Mikrowellen-Hintergrundstrahlung, bevor sie entdeckt wurde?

Um das herauszufinden, brauchen wir P(cosmic|Urknall) und P(cosmic|¬Urknall).

P(kosmisch|Urknall) hängt davon ab, welche Hilfsannahmen wir annehmen. Es mag einen Urknall gegeben haben, aber dann verursacht ein anderer Prozess die Auslöschung des kosmischen Mikrowellenhintergrunds.

P(cosmic|¬Urknall) ist sogar noch problematischer. „BigBang“ umfasst alle Modelle außer dem Big Bang-Modell. Einige werden einen kosmischen Mikrowellenhintergrund postulieren, andere nicht (und dies wird wiederum von Hilfsannahmen abhängen).

Darüber hinaus beinhaltet der Bayesianismus (nach Norton) eine falsche Präzision. Eine induktive Inferenz kann schwach, stark, sehr stark usw. sein. Aber oft können wir einen präzisen mathematischen Wert nicht angreifen.

Es gibt kein gemeinsames Maß für die Stärken induktiver Schlussfolgerungen in verschiedenen Bereichen. Vergleichen Sie: Curies Schlussfolgerung war stark, und die Schlussfolgerung von CMBR zu Urknall war stark.

Manchmal rechtfertigen die Hintergrundfakten die Verwendung formaler probabilistischer Ansätze. Denken Sie an radioaktiven Zerfall, DNA-Forensik, genetische Vererbung und Glücksspiele in Casinos.

Aber in Curies Schlussfolgerung mag es nicht einmal eine vorherige Wahrscheinlichkeit gegeben haben. Die Hypothese lautete: "Radiumchlorid hat eine monokline Kristallstruktur". Wissenschaftler waren diesbezüglich möglicherweise einfach unverbindlich.

Die Botschaft der materialen Theorie lautet: Induktive Regeln können nützlich sein, aber sie sind nur dann nützlich, wenn die relevanten faktischen Hintergrundbedingungen spezifiziert wurden und geeignet sind, die Anwendung dieser Regeln zu genehmigen. Also, ja, es gibt Fälle, in denen IBE oder Bayesianismus sehr mächtige Werkzeuge sind, aber sie können nicht allgemein als wissenschaftliches Denken angewendet werden.

Also: Ein Punkt, der die Materialtheorie begünstigt, ist, dass der formale Ansatz gescheitert ist. Niemand scheint in der Lage zu sein, die Induktionsregeln zu sagen, geschweige denn sie zu begründen.

Peden 2020: One reason for the attention it has drawn is that the theory retains some of the more attractive features of the predominant Bayesian approach, while discarding the more concerning.
AB HIER WEITER: http://www.thebsps.org/reviewofbooks/peden-on-norton/ .

Literaturverzeichnis
Norton, John D. (2009). Cosmology and Inductive Inference: A Bayesian Failure < https://www.researchgate.net/publication/36445551_Cosmology_and_Inductive_Inference_A_Bayesian_Failure>

Norton, John D. (2011). Challenges to Bayesian Confirmation Theory. In: Prasanta S. Bandyopadhyay und Malcolm R. Forster (Hrsg.): Handbook of the Philosophy of Science. Volume 7: Philosophy of Statistics. Amsterdam: Elsevier, S. 391 – 440.

Ein zweites Argument für die materiale Theorie ist, dass sie im Gegensatz zum formalen Ansatz die Daten leicht unterbringt. Die Unterschiede zwischen dem, was wir intuitiv als gute und schlechte Schlussfolgerungen erkennen, lassen sich leicht durch den materiellen Ansatz erklären, wie wir am Wismut- und Wachsbeispiel gesehen haben. Die Materialtheorie weist uns darauf hin, die Tatsachen zu betrachten, die die Induktion zulassen. Darüber hinaus entspricht die Materialtheorie eher der tatsächlichen wissenschaftlichen Praxis.

Während der formale Ansatz die induktiven Regeln nicht artikulieren konnte, berücksichtigt der materielle Ansatz die Daten.

Ein Aspekt davon ist, dass die Materialtheorie der wissenschaftlichen Praxis mehr entspricht. Ein wichtiger Teil der Wissenschaft ist die Kontrolle des induktiven Risikos. Wissenschaftler wollen das induktive Risiko minimieren.

Beim formellen Ansatz zur Induktion umfasst die Minimierung des induktiven Risikos zwei Schritte. Erstens müssen wir so viele Beweise wie möglich sammeln.

Zweitens müssen wir versuchen, unseren Katalog induktiver Regeln zu erweitern. Wir müssen wissen, was die guten induktiven Schemata sind, und Mittel haben, um ihren Grad an Zuverlässigkeit abzuschätzen. [Das machen wir mit Deduktion: Aristoteles-Syllogismen, Aussagenlogik, deontische Logik, temporale Logik, freie Logik usw.].

Doch obwohl Wissenschaft ein induktives Unternehmen ist und Wissenschaftler das induktive Risiko minimieren wollen, verbringen sie selten Zeit mit dem zweiten Schritt. Wissenschaftler versuchen selten, das induktive Schema zu artikulieren.

„Induktion ist der Ruhm der Wissenschaft und der Skandal der Philosophie.“ - C. D. D. Broad.

Wissenschaftler machen Induktionen und sie sind ziemlich gut darin, aber sie versuchen nicht explizit anzugeben, welchen induktiven Regeln sie folgen. Es sind Philosophen, die das tun.

Physiker und Biologen machen sich selten Gedanken darüber, was als Erklärung gilt, oder die Regeln, wann eine Erklärung besser ist als eine andere; Sie versuchen selten, alle ihre Schlussfolgerungen in den Bayes'schen Rahmen zu zwingen usw.

Nach der materialen Theorie besteht die Kontrolle des induktiven Risikos aus nur einem Schritt: dem Sammeln von Beweisen. Der Grund, warum Wissenschaftler sich nicht die Mühe machen, die universellen induktiven Regeln zu artikulieren, ist, dass sie damit nichts gewinnen würden.

Was ist die Begründung der Induktion? Induktive Schlüsse lassen sich nicht deduktiv begründen. Es ist möglich, dass die Prämissen wahr und die Schlussfolgerung falsch sind.

Was ist mit induktiv? Wir könnten es versuchen: Induktion war in der Vergangenheit erfolgreich, also wird sie auch in Zukunft erfolgreich sein. Aber dies ist ein Beispiel für genau die Regel, die wir rechtfertigen sollen!

Der übliche Weg, dies zu umgehen, besteht darin, sich auf eine allgemeine rechtfertigende Tatsache wie das Einheitlichkeitsprinzip zu berufen. UP ist so etwas wie: „Die Zukunft wird wie die Vergangenheit sein“ oder „Die Natur ist einheitlich“.

Wenn UP wahr ist, können wir uns auf Induktion verlassen. Die Tatsache, dass alles Wasser der Vergangenheit in Verbindung mit UP durstlöschend war, rechtfertigt die Erwartung, dass alles zukünftige Wasser durstlöschend sein wird.

„Der Satz, dass die Natur uniformiert ist, ist das Grundprinzip oder das allgemeine Axiom der Induktion.“ - John Stuart Mill.

(1) Alle induktiven Schlüsse setzen UP voraus.
(2) UP ist nicht deduktiv gerechtfertigt – es ist logisch möglich, dass eine gegebene Einheitlichkeit in Zukunft nicht gegeben ist.
(3) UP wird nicht induktiv begründet – gemäß (1), und die induktive Begründung von UP müsste selbst UP voraussetzen, wäre also eindeutig zirkulär.
(4) Andere Rechtfertigungsmittel stehen nicht zur Verfügung.
(5) Es gibt keine Rechtfertigung für UP.
(6) Es gibt keine Rechtfertigung für die Induktion.

Die materiale Theorie lehnt Prämisse (1) ab. Es gibt kein allgemeines Prinzip, das allen induktiven Schlussfolgerungen zugrunde liegt: Jede Induktion ist lokal und basiert auf spezifischen Fakten.

Selbst wenn wir UP etablieren könnten, würde es uns nicht helfen, eine bestimmte induktive Schlussfolgerung zu verstehen.

Die Welt ist nur in gewisser Hinsicht einheitlich, und UP an sich hilft uns nicht, die Einheitlichkeiten zu identifizieren. Selbst wenn wir eine Rechtfertigung für UP hätten, könnte es nicht diese Machtinduktion sein.

Problem: Es stimmt zwar, dass es in der Materialtheorie keine skeptische Anfechtung induktiver Regeln gibt (weil es keine induktiven Regeln gibt), aber jede spezifische induktive Schlussfolgerung kann immer noch in Frage gestellt werden.

Die Wismut-Inferenz wird durch das materielle Postulat genehmigt, dass Elemente in Bezug auf die Schmelztemperatur einheitlich sind. Aber was rechtfertigt diesen Glauben? Haben wir also wirklich etwas gelöst? Laut Norton gibt es hier also keine nennenswerten Schwierigkeiten.

Eine Induktion wird durch ein materielles Postulat genehmigt; der Glaube an das materielle Postulat basiert auf einer Induktion, die von einem anderen materiellen Postulat genehmigt wurde; und so weiter... Tatsachen gründen auf weiteren Tatsachen.

„Wir induzieren eine Tatsache mit einer Induktion, die durch die Tatsachen eines materiellen Postulats begründet ist. Diese letzteren Tatsachen werden durch Induktionen gerechtfertigt, die wiederum durch die Tatsachen anderer materieller Postulate begründet sind, und diese Tatsachen werden durch Induktion gerechtfertigt, die durch andere Tatsachen begründet ist und so weiter" - John Norton.

Damit bleibt die Frage, wie diese Begründungsketten enden. Hier ´gibt´ es ein skeptisches Problem. Aber es ist nicht das Problem der Induktion. Es ist Aggripa´s Trilemma.

Für jede Begründungskette entweder:

(1) es endet in grundlegenden Überzeugungen, die nicht durch andere Überzeugungen gerechtfertigt sind, oder
(2) es ist kreisförmig, oder
(3) es geht unendlich zurück.

Alle diese Optionen sind problematisch. Aber diese Herausforderung stellt sich auch für die Rechtfertigung des Abzugs und für alles andere, was wir versuchen könnten zu rechtfertigen.

Dies ist ein allgemeines Rechtfertigungsproblem, es würde sich beispielsweise für den Versuch ergeben, deduktive Regeln zu rechtfertigen. Dieses Problem wird bei jeder Überzeugung auftreten, die Sie haben, nicht nur bei Überzeugungen, die durch Induktion gebildet werden, also ist dies nicht das Problem. Das Problem, mit dem die Materialtheorie konfrontiert ist, ist also nur das allgemeine Problem der Rechtfertigung, mit dem alle Überzeugungen konfrontiert sind. Es ist ein allgemeines Rechtfertigungsproblem im Allgemeinen, es ist kein spezifisches Problem.

Beim formalen Induktionsansatz besteht die Herausforderung darin, dass eine deduktive Begründung zu stark ist, während eine induktive Begründung kreisförmig wäre.

In der materialen Theorie sind induktive Schlussfolgerungen durch Fakten gerechtfertigt.

Der rechtfertigende Umstand wird in der Regel induktiv begründet. Aber hier gibt es keine problematische Zirkularität, da die rechtfertigende Tatsache sich von der Schlussfolgerung unterscheidet.

Der formale Ansatz verwendet eine Induktionsregel, um die Induktionsregel zu rechtfertigen. Eine induktive Regel wird durch UP gerechtfertigt, aber UP kann nur durch die induktive Regel gerechtfertigt werden.

Die materiale Theorie verwendet ein Gesicht, um eine bestimmte Tatsache zu rechtfertigen. „Alles Wismut schmilzt bei 271°C“ wird durch Beobachtungen von Wismut und die Tatsache gerechtfertigt, dass Elemente eine einheitliche Schmelztemperatur haben.

"Elemente haben eine einheitliche Schmelztemperatur" wird durch eine eindeutige Tatsache gerechtfertigt.

Auch hier scheint die wissenschaftliche Praxis so zu funktionieren. Kein Wissenschaftler interessiert sich für die Beantwortung des Induktionsproblems von Hume. Wenn eine bestimmte induktive Schlussfolgerung abgefragt wird, wird ein Wissenschaftler antworten, indem er die Fakten zitiert, die die Schlussfolgerung zulassen. und ja, es wird hier eine Art Rückschritt geben, wenn wir nach der Begründung eines materiellen Postulats fragen, werden andere Tatsachen angeführt. Und dann können wir nach der Rechtfertigung für diese Tatsachen fragen und so weiter. Aber daran ist nichts Fantasievolles. Es wird nur darum gehen, die Wissenschaftsgeschichte im Grunde richtig zu artikulieren oder (wahrscheinlicher) eine stromlinienförmige Darstellung von Beweissicherungsbeziehungen in der Wissenschaft zu artikulieren, wie sie in naturwissenschaftlichen Lehrbüchern zu finden sind. Wenn Sie eine wissenschaftliche Tatsache angeben und jemand Sie fragt, was die Rechtfertigung dafür ist, geben Sie eine andere Tatsache an, die von der Wissenschaft festgestellt wurde. Und wenn sie dich nach der Begründung dafür fragen, kannst du eine andere Tatsache angeben. So wie es wissenschaftliche Lehrbücher tun.

Die Behauptung lautet also: Die materielle Theorie der Induktion stellt sich dem Induktionsproblem nicht. Und wenn es stimmt, ist dies ein bedeutender Punkt zu seinen Gunsten.

Kann damit auch Hempels Paradoxon, Goodmans Paradoxon, usw. gelöst werden???

Literaturverzeichnis
Norton, John D. (2003a). A Material Theory of Induction. Philosophy of Science 70(4), S. 647 - 670.
Norton, John D. (2014). A Material Dissolution of the Problem of Induction. Synthese 191(4), S. 671 - 690.

-

Norton (2014) spricht passenderweise von "Dissolution" (Auflösung) statt von "Solution" (Lösung) des logischen Induktionsproblems.

Peden 2022: Norton stimmt zu, dass Hintergrundwissen über Zuverlässigkeit wichtig ist, weist jedoch die traditionelle Ansicht zurück, dass es allgemeine Annahmen sind, die gute Induktionen rechtfertigen. Keine plausible Annahme dieser Art wird ausreichen, um die Zuverlässigkeit zu bestätigen. Stattdessen werden Induktionen durch kontextspezifisches Hintergrundwissen begründet. Beispielsweise kann die Konformität beobachteter Gasproben mit dem Gesetz von Boyle aufgrund spezifischer Tatsachenbehauptungen in der Kontinuumsmechanik und anderen wissenschaftlichen Entdeckungen über Gase auf alle Gasproben extrapoliert werden, nicht aufgrund eines allgemeinen Einheitlichkeitsprinzips. Typischerweise bietet dieses kontextspezifische (oder „lokale“) Hintergrundwissen keine deduktive Gewissheit, aber es muss die Hypothese rechtfertigen, dass unsere beobachteten Stichproben wahrscheinlich repräsentativ für die Zielpopulation unserer Inferenz sind. Damit lenkt Norton die Aufmerksamkeit weg von der Rechtfertigung von Behauptungen, allgemeine Formen der induktiven Argumentation seien zuverlässig. Stattdessen ergibt sich die Rechtfertigung aus dem Wissen, dass der Gegenstand eines induktiven Arguments so beschaffen ist, dass unsere Beobachtungen ein zuverlässiger Leitfaden für unsere Schlussfolgerungen sind.

Nortons Beispiele beinhalten induktive Schlussfolgerungen in Fällen, in denen wir über eine beträchtliche Menge an fundiertem Hintergrundwissen verfügen.

Aber wie gewinnen wir dieses Hintergrundwissen überhaupt? Dies ist wichtig, da die Induktion nur dann durch Tatsachen genehmigt werden kann, wenn diese Tatsachen bekannt sind. Hier gibt es zwei eng miteinander verbundene Sorgen.

(1) Historisch: Verfolgen Sie die Praxis der induktiven Schlussfolgerungen zurück, und wir kommen schließlich zur allerersten Induktion.

Betrachten Sie den Fall, bevor jemand eine induktive Schlussfolgerung zieht. Nennen Sie die Gesamtheit des nicht-induktiven Wissens N. Wie können wir einen Schluss über N hinaus ziehen? Die Sorge ist, dass es nichts gäbe, was man als materielles Postulat verwenden könnte.

Norton antwortet: Aber dieses Szenario ist eine Idealisierung. Es ist äußerst unwahrscheinlich, dass es jemals einen Punkt gab, an dem Menschen nur nicht-induktive Überzeugungen hatten. Jede Gesellschaft hat eine Vielzahl von allgemeinen Überzeugungen über die Welt, die auf eine Vielzahl von manchmal zuverlässigen, manchmal unzuverlässigen Weisen entstanden sind.

Als die Menschen die Unterscheidung zwischen Deduktion und Induktion formulierten, hatten sie bereits verschiedene allgemeine Überzeugungen, die sie als materielles Postulat in induktiven Schlüssen verwenden konnten.

(2) Begründung. Die historische Geschichte illustriert einfach das Problem, das die Unterstützungsbeziehungen unseres gegenwärtigen Wissens betrifft. Empirisches Wissen basiert auf Erfahrung. Aber die Erfahrung allein liefert kein materielles Postulat, das einen induktiven Schluss auf eine allgemeine Überzeugung jenseits der Erfahrung zulassen könnte.

Offensichtlich machen Menschen tatsächlich induktive Schlussfolgerungen jenseits der Erfahrung. Materialtheoretisch ist dies aber nicht zu rechtfertigen, weil die Erfahrung die richtigen Materialpostulate nicht liefern kann.

Nortons Antworten: Erstens, kann Erfahrungswissen nicht strikt vom Wissen über die Welt abgegrenzt werden. Es gibt keine Reihe von Aussagen, die allein den Inhalt der Erfahrung ausdrücken [Quine: Semantischer Holismus].

Nehmen Sie "der Ball ist rot". Dies ruft die Konzepte "Ball" und "Rot" hervor. Um den Begriff "Ball" zu haben, benötigen wir ein Verständnis der Geometrie, der elastischen Eigenschaften von Materialien und dynamischer Bewegungen.

Die angemessene Anwendung eines Konzepts wie "rot" wird durch die Auseinandersetzung mit einer Reihe von externen Objekten erlernt; eine Person versteht das Konzept nicht, wenn sie einen roten Ball nicht von einem rosa Ball unterscheiden kann.

Zweitens haben nach Nortons Ansicht die rechtfertigenden Beziehungen zwischen Überzeugungen keine einfache hierarchische Form. Norton ist eher ein Kohärentist als ein Fundamentalist.

In der Praxis gehen wir von einer Vermutung aus. Wir geben eine Behauptung ohne überzeugende Begründung nur vorläufig weiter und verwenden sie, um verschiedene Schlussfolgerungen zuzulassen, sodass wir verschiedene Überzeugungen über die Welt aufbauen.

Wir müssen dann später auf die anfängliche Vermutung zurückkommen und zeigen, wie sie durch etablierte Überzeugungen gestützt werden kann.

Beispiel: "Wir haben am Ende eine Struktur, in der jeder rechtfertigende Fakt durch andere induktive Schlussfolgerungen in einer hochgradig verbundenen, massiv verworrenen Struktur gestützt wird."

Wissen ist laut Norton wie ein ausgeklügelter Steinbogen strukturiert: Aussagen über Erfahrung sind analog zum Grundgestein, und dann erhält jeder Stein / jede Aussage darüber Unterstützung von allen Steinen um ihn herum, nicht nur von den Steinen darunter.

Die Verwendung vorläufiger Hypothesen ist analog dazu, wie wir Gerüste verwenden, um den Bogen zu bauen. Sobald der Bogen fertig ist, wird das Gerüst entfernt.

Die vorläufige Hypothese ist ein Gerüstsatz: Wir wetten darauf, sehen, ob es funktioniert. Wenn es nützliche Schlussfolgerungen erlaubt, können wir später darauf zurückkommen und zeigen, wie es durch Überzeugungen gerechtfertigt ist, die jetzt gut etabliert sind. Dadurch wird das Gerüst entfernt.

.

Mill, John Stuart ([1872] 1916), A System of Logic: Ratiocinative and Inductive: Being a Connected View of the Principles of Evidence and the Methods of Scientific Investigation, 8th ed. London: Longman, Green, and Co.

Norton, John D. (2003a). A Material Theory of Induction. Philosophy of Science 70(4), S. 647 - 670.

Norton, John D. (2003b). The Formal Equivalence of Grue and Green and how it undoes the New Riddle of Induction. Preprint. <http://philsci-archive.pitt.edu/1356/>

Norton, John D. (2005). A Little Survey of Induction. In: Peter Achinstein (Hrsg.): Scientific Evidence: Philosophical Theories and Applications. Baltimore: Johns Hopkins University Press, S. 9 – 34.

Norton, John D. (2006). Induction without Probabilities. Preprint. <http://philsci-archive.pitt.edu/3107/>

Norton, John D. (2007). History of Science and the Material Theory of Induction: Einstein’s Quanta, Mercury’s Perihelion. European Journal for Philosophy of Science 1(1), S. 3 – 27.

Norton, John D. (2009). Cosmology and Inductive Inference: A Bayesian Failure < https://www.researchgate.net/publication/36445551_Cosmology_and_Inductive_Inference_A_Bayesian_Failure>

Norton, John D. (2010a). Deductively Definable Logies of Induction. Journal of Philosophical Logic 39(6), S. 617 - 654.

Norton, John D. (2010b). A Survey of Inductive Generalization. Preprint. <https://sites.pitt.edu/~jdnorton/papers/Survey_ind_gen.pdf>

Norton, John D. (2010c). There are no Universal Rules of Induction. Philosophy of Science 77(5), S. 765 – 777.

Norton, John D. (2011). Challenges to Bayesian Confirmation Theory. In: Prasanta S. Bandyopadhyay und Malcolm R. Forster (Hrsg.): Handbook of the Philosophy of Science. Volume 7: Philosophy of Statistics. Amsterdam: Elsevier, S. 391 – 440.

Norton, John D. (2014). A Material Dissolution of the Problem of Induction. Synthese 191(4), S. 671 - 690.

Norton, John D. (2019). A Demonstration of the Incompleteness of Calculi of Inductive Inference. British Journal for the Philosophy of Science 70(4), S. 1119 - 1144.

Norton, John D. (2021). The Material Theory of Induction. Calgary: University of Calgary Press.

This book is published open access through the new BSPS Open book series, the new outlet for cutting edge philosophy of science monographs that publishes Open Access at no cost to authors or readers. Watch a video about BSPS Open or read more here. So you don´t have to spend 120€ for it.

Bayesianismus
Bestätigung
Induktion
Induktionsproblem
Seungbae Park: Die Optimistische Meta-Induktion
Schluss auf die beste Erklärung

danach: Ordner kopieren in: "Das Super-Wunderargument gegen den (Super-)Humeanismus".

zum vorherigen Blogeintrag                                        zum nächsten Blogeintrag 

Liste aller Blogbeiträge zum Thema "Logik"